Optimization¶

import some modules¶

[1]:

from dftpy.ions import Ions
from dftpy.field import DirectField
from dftpy.grid import DirectGrid
from dftpy.functional import LocalPseudo, Functional, TotalFunctional
from dftpy.formats import io
from dftpy.math_utils import ecut2nr
from dftpy.time_data import TimeData
from dftpy.optimization import Optimization
from dftpy.mpi import sprint

pseudopotential file¶

[2]:

path_pp='../DATA/'
file1='Al_lda.oe01.recpot'
PP_list = {'Al': path_pp+file1}

build the ions or read from file¶

[3]:

from ase.build import bulk
atoms = bulk('Al', 'fcc', a=4.05, cubic=True)
ions = Ions.from_ase(atoms)
# ions = io.read(posfile)

make a grid¶

[4]:

nr = ecut2nr(ecut=35, lattice=ions.cell)
grid = DirectGrid(lattice=ions.cell, nr=nr)
sprint('The final grid size is ', nr)

The final grid size is  [20 20 20]

build local pseudo, and generate guess density¶

[5]:

PSEUDO = LocalPseudo(grid = grid, ions=ions, PP_list=PP_list)

rho_ini = DirectField(grid=grid)
rho_ini[:] = ions.get_ncharges()/ions.cell.volume

setting key: Al -> ../DATA/Al_lda.oe01.recpot

instance KEDF, XC and HARTREE functionals¶

[6]:

KE = Functional(type='KEDF',name='TFvW')
XC = Functional(type='XC',name='LDA')
HARTREE = Functional(type='HARTREE')

instance DFTpy evaluator¶

[7]:

evaluator = TotalFunctional(KE=KE, XC=XC, HARTREE=HARTREE, PSEUDO=PSEUDO)

instance and execute DFTpy density optimizer¶

[8]:

optimization_options = {'econv' : 1e-6*ions.nat}
opt = Optimization(EnergyEvaluator=evaluator, optimization_options = optimization_options,
        optimization_method = 'TN')

rho = opt.optimize_rho(guess_rho=rho_ini)

Step    Energy(a.u.)            dE              dP              Nd      Nls     Time(s)
0       -8.090977705021E+00     -8.090978E+00   7.877088E-01    1       1       3.019786E-02
1       -8.273226046266E+00     -1.822483E-01   7.033209E-02    2       1       4.573035E-02
2       -8.280858134980E+00     -7.632089E-03   4.803545E-03    7       1       7.858968E-02
3       -8.281101057269E+00     -2.429223E-04   3.640539E-04    5       1       1.080880E-01
4       -8.281135973281E+00     -3.491601E-05   3.590568E-05    6       1       1.483943E-01
5       -8.281138620008E+00     -2.646726E-06   2.500516E-06    5       1       1.792736E-01
6       -8.281138990521E+00     -3.705134E-07   4.570800E-08    8       1       2.268357E-01
#### Density Optimization Converged ####
Chemical potential (a.u.): 0.3011519653615224
Chemical potential (eV)  : 8.194761599521389

evaluate final energy¶

[9]:

energy = evaluator.Energy(rho=rho, ions=ions)
print('Energy (a.u.)', energy)

Energy (a.u.) -8.281138990520986

print the timing¶

[10]:

TimeData.output(lprint=True, sort='cost')

--------------------------------Time information--------------------------------
Label                       Cost(s)                 Number          Avg. Cost(s)
ewald.Energy_corr           0.0001                  1               0.0001
CBspline._calc_PME_Qarray   0.0017                  1               0.0017
ewald.Energy_rec_PME        0.0026                  1               0.0026
LocalPseudo.local_PP        0.0029                  1               0.0029
ewald.Energy_real_fast2     0.0050                  1               0.0050
ewald.energy                0.0078                  41              0.0002
TF                          0.0196                  41              0.0005
InvFFT                      0.0225                  83              0.0003
FFT                         0.0277                  84              0.0003
Hartree.compute             0.0351                  41              0.0009
vW                          0.0436                  41              0.0011
LibXC                       0.0893                  41              0.0022
Optimize                    0.2290                  1               0.2290

[11]:

rho.write('rho.xsf', ions=ions)
rho.write('rho.cube', ions=ions)

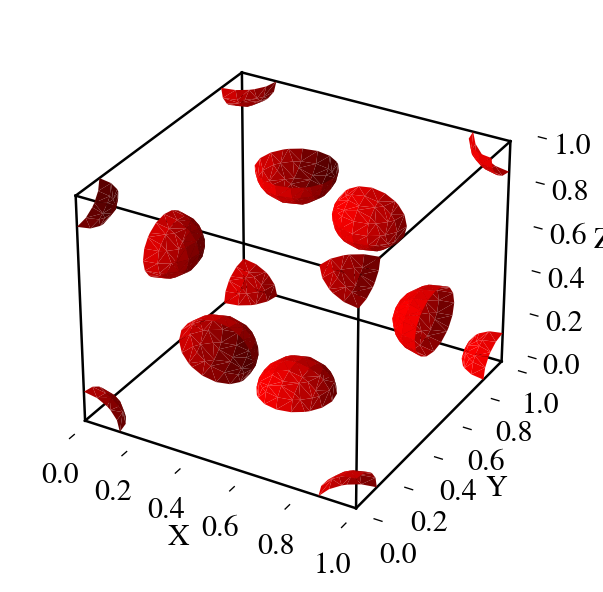
Visualize with scikit-image and matplotlib¶

!pip install scikit-image matplotlib

[12]:

from dftpy.visualize import view

[13]:

# %matplotlib widget
view(data=rho)

../../_images/tutorials_jupyter_density_optimization_25_0.png

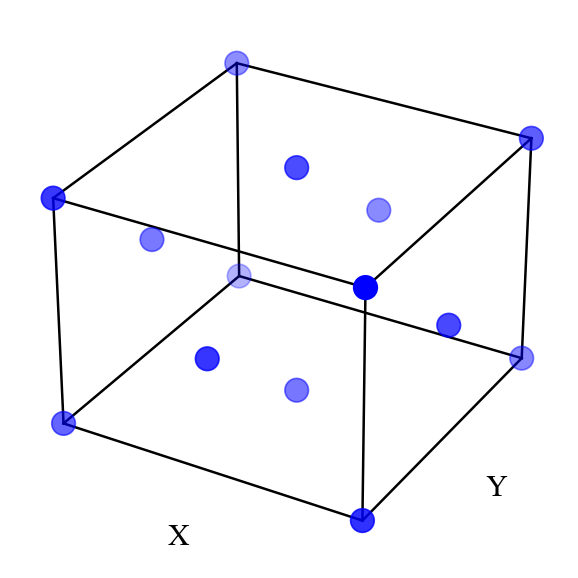
[14]:

view(ions=ions)

../../_images/tutorials_jupyter_density_optimization_26_0.png

Visualize with VESTA¶

[15]:

# view(ions=ions, data=rho, viewer='vesta')